Math - Linear Equations

$2x + 1 = 3x - 1$

A linear equation is an equation that describes a relationship with a constant rate of change, forming a straight line.

Key Characteristics of Linear Equations

• Degree of 1: The highest power of any variable is 1.  
• No products of variables: There are no terms like $xy$, $x^2y$, or similar combinations.  
• Straight line graph: When plotted on a coordinate plane, it forms a straight line.

Examples of Linear Equations

$2x + 3y = 7$
$y = 5x - 2$
$x = 4$

Examples of Non-linear Equations

$x^2 + y^2 = 25$
$y = 2x^3 - 1$
$1/x + y = 3$

Solving Linear Equations

A great way to master linear equations is by practicing:
GeoGebra - Linear Equation Generator

$2x - 3 = -7$

$2x - 3 = -7\\ 2x - 3 + 3 = -7 + 3\\ 2x = -4\\ \frac{2x}{2} = \frac{-4}{2}\\ \frac{\cancel{2}x}{\cancel{2}} = \frac{-4}{2}\\ x = -2$

$x(3+1) = 2(x+1)$

$x(3+1) = 2(x+1)\\ 3x + x = 2x + 2\\ 4x = 2x + 2\\ 4x - 2x = 2x - 2x + 2\\ 2x = 2\\ \frac{2x}{2} = \frac{2}{2}\\ \frac{\cancel{2}x}{\cancel{2}} = \frac{2}{2}\\ x = 1$

$\frac{-x+6}{3} = -x + 3$

$\frac{-x+6}{3} = -x + 3\\ 3 * \frac{-x+6}{3} = 3(-x+3)\\ \cancel{3} * \frac{-x+6}{\cancel{3}} = 3(-x+3)\\ -x+6 = -3x + 9\\ -x+6-6 = -3x+9-6\\ -x = -3x + 3\\ -x + 3x = -3x + 3x + 3\\ 2x = 3\\ \frac{2x}{2} = \frac{3}{2}\\ \frac{\cancel{2}x}{\cancel{2}} = \frac{3}{2}\\ x = 1.5$

Graphing Linear Equations

The best way to graph a linear equation is to write the equation in slope-intercept form.

$y = mx + b$

Graphing Linear Equations (youtube)
Graphing Linear Equations in Two Variables (palmbeachstate.edu)

Examples

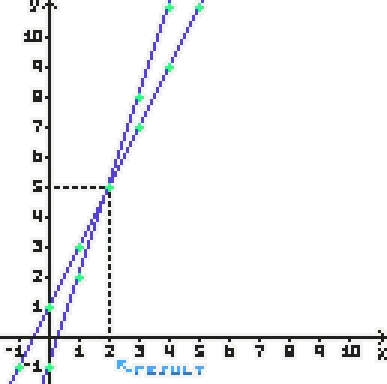
$4x - 7 = 21\\ y = 4x - 7$

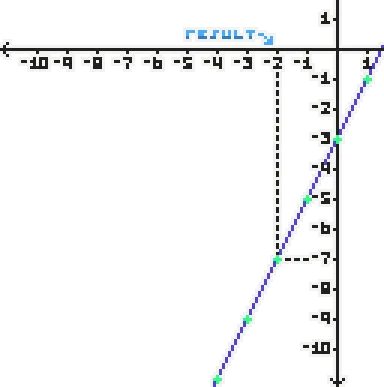
$7x + 9 = 3(x + 2) + 1\\ y_1 = 7x + 9\\ y_2 = 3x + 7$

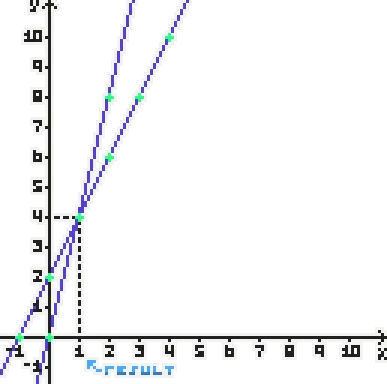
$y - 5x = x + 5\\ y - 5x + 5x = 5x + 1x + 5\\ y = 6x + 5$

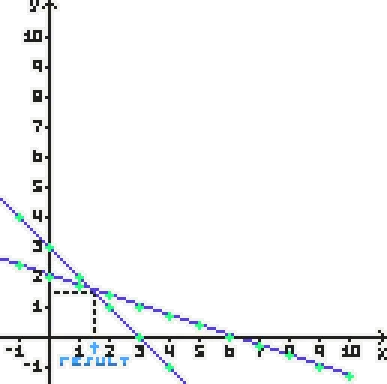
$3x + 4y = 18\\ 3x - 3x + 4y = -3x + 18\\ 4y = -3x + 18\\ \frac{4y}{4} = \frac{-3x + 18}{4}\\ \frac{\cancel{4}y}{\cancel{4}} = \frac{-3x + 18}{4}\\ y = \frac{-3x + 18}{4}$